Hugh Osmond recently put out this interesting twitter thread:
Although the average age of death in the UK is around 82, if
a person reaches 82 then on average (i.e. without knowing any details of the
particular person) the person can expect to live about another 8 years. We know
the average age of a person dying from Covid is also 82, so it seems reasonable
to assume that a typical person dying from Covid loses 8 life years. But, as Hugh
points out, this reasoning is flawed. Hugh provides what is essentially an informal argument. In what follows we provide a formal explanation.
The question we are trying to answer is:
Knowing that an individual (let’s say it’s a man called Fred) has died from Covid at the age of 82, how much longer would Fred have lived if he had not got Covid?
This is a classic ‘counterfactual’ question. We want to know what would happen to Fred in an alternative world if something that happened in the real world (namely, getting Covid) was changed. And we want to take account of everything we can learn about Fred that will be unchanged in the counterfactual world from what happened in the real world.
Crucially, because we know that Fred died of Covid, we learn from the real world that (compared to the average 82 year-old) Fred is much more likely to also have had some critical pre-existing illness. And this knowledge must be retained in the counterfactual world.
As very well explained by Judea Pearl, answering counterfactual questions requires a causal model and an inference method that are beyond what can be achieved with traditional statistical methods. In what follows we use illustrative and simplified assumptions to explain this counterfactual reasoning.
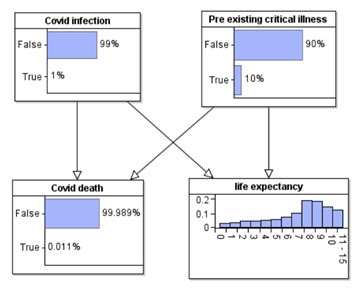
First, we need a causal model of the ‘real world’. Such a basic causal model is shown in Figure 1.
Figure 1 Basic causal model (for 82 year-olds)
This tells us that whether a person suffers a Covid death depends not just on whether the person becomes infected, but also on many other factors including whether the person has a pre-existing critical illness. Similarly, a person’s life expectancy depends on the same factors (among others).
When we assign prior probabilities to the nodes ‘Covid infection’ and ‘Pre-existing critical illness’, and conditional probabilities to the nodes ‘Covid death’ and ‘life expectancy’, then the causal model becomes a Bayesian network for which we can perform Bayesian inference.
In what follows we use the following assumed prior and conditional probabilities:
- Covid infection: 1%
- Pre-existing critical illness: 10%
- Covid death given Covid infection is false = 0%
- Covid death given Covid infection and Pre-existing critical illness = 10%
- Covid death given Covid infection and no Pre-existing critical illness = 0.1%
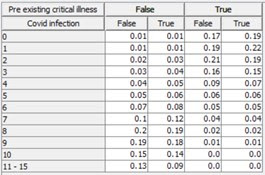
- The full set of conditional probabilities for life expectancy is given in Table 1
Table 1 Conditional probability table for 'life expectancy'
Changing any of these probability assumptions (within reason) does not change the thrust of the argument (readers are free to try out the model and make their own changes using their favourite Bayesian network software**).
With these assumptions we get the prior marginal probabilities shown in Figure 2.
So, in the real world the median life expectancy of an average 82-year-old is 8 years.
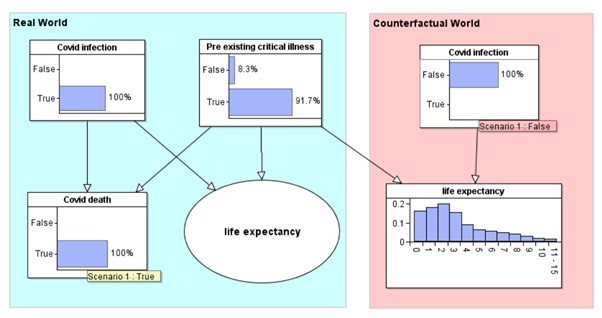
But, if we know that an individual dies from Covid then, while obviously this means that ‘Covid infection’ must be true, through Bayesian inference we also get the revised probability for ‘pre-existing critical illness’ shown in Figures 3.
Figure 3 Revised probabilities are observing Covid death
We can now use this new information about the probability this individual has pre-existing critical illness in a counterfactual world where he is not infected with Covid. The counterfactual model required for this is shown in Figure 4.
Figure 4 Counterfactual world
The ‘Covid infection’ and ‘life expectancy’ nodes in the counterfactual world are simply copies of the same named nodes from the real world model. They have exactly the same prior and conditional probability tables respectively. When we enter ‘Covid infection’ is false in the counterfactual world, we get the revised probability distribution for life expectancy. This individual has a median of 2 years life expectancy, rather than the 8 years.
The inference performed in this counterfactual model is not possible using the original model alone.
For more information on Bayesian networks
and counterfactual reasoning see our book and short videos.
**The model used here can be downloaded and run in the free trial version of AgenaRisk (we declare an interest - Directors of the company that owns the software).
29 Jan update: Here is a 5 minute video explanation on the above with an even simpler model (that can be downloaded by right clicking)



Excellent article. The number of serious health issues has been fairly well documented as well.
ReplyDeletehttps://www.cdc.gov/pcd/issues/2021/pdf/21_0123.pdf
Well done. YLL was always the best metric as it captures the fact that fatal harms that might occur from lockdown, vaccines, etc are going to shift harm to younger age groups. Never once even heard YLL mentioned in the media.
ReplyDeleteIn short, it's about nursing homes: 50% of deaths, 1% of population, remaining average life expectancy less than one year.
ReplyDeleteBut let's not ignore the other 50% who still had a much longer healthy life ahead of them.
DeleteMethinks you missed the point Michael Kay
DeleteEven though it does not change the inference results at all, there is obviously also a causal link from Covid Death to Life Expectancy
ReplyDeleteI am wondering if there are data anywhere available with which we could train the Bayesian Network after having defined the causal model of the ‘real world’ according to Figure 1 ?
ReplyDeleteHi Guys, but the model you use is not really a structural causal model, which should contain only structural equations in the internal nodes; so isn't your counterfactuals likely incorrect to some extent??
ReplyDeleteI just read Hugh Osmond's recent Twitter thread, and it's certainly thought-provoking. He discusses how medical diagnoses of COVID victims indicated that many had a very short life expectancy, which adds a different perspective to the overall conversation. On a lighter note, I've been diving into tech lately and I've found that the best platform for mobile app development can make a big difference when working on new projects. It's amazing how many tech and health discussions are developing at the same time!
ReplyDeleteI was revisiting this post. Does the free trial version have this model? I have the free version but I could not locate it. I have a version using NETICA. Many thanks.
ReplyDeleteThis is cool as f'ck, I found great blog. God Bless you man. Have a nice day... MM
ReplyDeleteYour content is brilliant story in many ways. This is good. Thankyou for sharing!... MM
ReplyDeleteKeep up the good work you are doing here. Good job! Nice article you made... MM
ReplyDeleteFound this interesting post to read. I really enjoy it!! Pretty great article... MM
ReplyDeleteBrief but Very accurate information. A must read post. Thanks for make it free.. MM
ReplyDelete
ReplyDeleteexcellent publish, very informative.
ReplyDeleteI ponder why the other specialists of this sector don’t notice this.
ReplyDeleteYou should proceed your writing. I am confident, you’ve a great readers’ base already!
ReplyDeleteIt is typical to encounter difficulties when using assignment writing services.
ReplyDeleteOne of the most serious issues is a lack of good communication.