This makes interesting reading for anybody who still believes the Government 'case' data and the claim that just because you don't have any COVID-19 symptoms it doesn't mean you aren't in danger (and a danger to others)....
This data also means that if the Government claim that “1 in 3 people with the virus has no symptoms” is correct then the ONS estimated infection rate is massively inflated - the currently reported ‘case’ numbers must be at least 11 times greater than the true number of cases. On the other hand, if the Government estimates of case numbers are correct then at most 1 in 34 people with the virus has no symptoms. Here's why:
Cambridge has a population of 129,000.
If the ONS infection estimates for Cambridge (0.71%) are accurate, then during an average week in this period about 916 people had the virus and 128,084 did not.
But if the “1 in 3” claim is correct about 305 of the 916 people in Cambridge with the virus were asymptomatic and 611 had symptoms.
While we do not know how many people in total in Cambridge were asymptomatic, we can certainly assume there must have been at most 128,389 (namely 129,000 minus the 611 we know had symptoms). So, with 305 asymptomatics having the virus, that means at least 305/128389 people with no symptoms had the virus. That is at least 0.24% (i.e. at least around 1 in 421).
But the study shows on average only 1 in 4867 (0.0205%) asymptomatics had the virus. So, we should have found at most 26 asymptomatics with the virus not 305.
That means the “1 in 3” claim and the ONS estimates cannot both be correct.
If the “1 in 3” claim is correct, then the maximum possible value for the infection rate is at most 0.062% and not 0.71% as claimed. So the ONS estimated infection rate would be 11 times greater than the true rate. (Formal proof below)
On the other hand, if the ONS reported infection of 0.71% is correct, then at most 2.95% (1 in 34) of people with the virus have no symptoms and not 1 in 3 as claimed. (Formal proof below)
Conclusions:
- Although the above analysis applied to a single UK city, there is no reason to believe it' is special (see the report below on national lateral flow testing data).
- Since mass PCR testing began many of those classified as 'cases' were not COVID-19. And the Government claim that "1 in 3 with the virus has no symptoms" is massively exaggerated. There needs to be confirmatory testing for any people testing positive before they are declared a 'case'.
- We should stop testing people without symptoms unless they have been in recent contact with a person confirmed as having the virus.
- And it's always interesting to compare number of NHS 999 emergency COVID-19 calls/triages with number of 'cases'. This data (digital.nhs.uk/dashboards/nhs) clearly shows real pandemic last spring but not '2nd/3rd waves'. All caveats discussed here probabilityandlaw.blogspot.com/2021/01/more-o apply
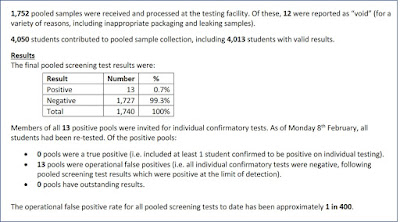
Also: This Government report says 9,480 of 2,372,358 lateral flow tests in UK 28 Jan - 3 Feb were positive. It is assumed almost all lateral flow tests are on people without symptoms. Given the false positive rate for these tests that's about 1 in 1587 true positives. In the same period the ONS estimated UK infection rate was 1 in 77.
Obviously all of this data is on asymptomatics tested, so we expect the percentage testing positive to be less than the overall infection rate. However, this data still massively contradicts Government claims about asymptomatics as explained here.
And, of course, we have very solid evidence that the number of 'cases' based on PCR testing are inflated.
The links:
- Cambridge Study
- ONS estimates
- About pooled testing
- Implications to the Government's claim that "1 in 3 people with the virus has no symptoms"
- On the importance of confirmatory testing