28 Feb 2021 DRAFT ONLY: This article is under review and will be updated. An updated analysis with new data from the Cambridge study is here
One of the major messages currently being pushed everywhere by the UK Government about COVID-19 is the claim that "1 in 3 people who have the virus have no symptoms".
A person is classified as having COVID if they get a positive test result and it has long been conjectured that (for PCR tests) many of these are false positives especially for people who have no symptoms and where there was no confirmatory test (the new evidence below provides further confirmation of this). So, clearly, it is possible that a large proportion of people classified as having the virus (as opposed to actually having the virus) have no symptoms. But, the new evidence suggests that either the "1 in 3" proportion is massively
exaggerated, or the 'case' numbers are massively exaggerated. Or
(likely) a combination of both. They certainly cannot both be true. In fact, if we accept that the Government case numbers really are people who have the virus then (based on the new evidence) it turns out that between 1 in 56 and 1 in 13 people who have the virus have no symptoms - very different from the Government "1 in 3" claim. Conversely, if the "1 in 3 claim" was really correct, than it turns out that the proportion of people with the virus during 1-7 Feb was not 1.25%, i.e. 1 in 80 as claimed, but between 0.09% and and 0.29% (i.e. between 1 in 1,111 and 1 in 345).
To understand what it going on here, it is important first to note that many people who see a statement like
"1 in 3 people who have the virus have no symptoms"
assume this is the same as:
"1 in 3 people who have no symptoms have the virus".
That is, in fact, a classic probability fallacy called the fallacy of the transposed conditional (or prosecutor's fallacy) whereby the probability of a hypothesis H given some evidence E is assumed to be equal to the probability of the evidence E given the hypothesis H. It is not. Just think of the example where an animal is hidden behind a screen. Let H be the hypothesis that the animal is a cow. We know that almost every cow has 4 legs (we allow for a few who have lost legs). So if I give you the evidence E that the cow has 4 legs then the probability of the evidence E given H is 1 (or very close to it). But the probability of H given E (i.e. the probability the animal is a cow given that the animal has 4 legs) is certaintly not close to 1 since most 4-legged animals are not cows.
Perhaps the Government "1 in 3" message was phrased in the way it was to deliberately exploit this very common misunderstanding. Obviously, it is not the case that "1 in 3 people who have no symptoms have the virus", because even if as few as a half the UK population does NOT currently have COVID-symptoms, then there would be over 11 million people who have the virus but no symptoms. This is clearly wrong, since the ONS estimate for total active cases for the week ending 6 Feb is that less than one million people (1.25% of the population) have the virus (in any case, as we explain below, we believe the 1.25% is too high anyway because of the inclusion of false positives).
The new evidence that suggests that both the case numbers, and the claim that "1 in 3 people who have the virus have no symptoms", are exaggerated comes from an ongoing study at Cambridge University. This study tests students without symptoms and, for the
week of 1-7 Feb, they reported that a total of 4058 students with no symptoms
were tested. None of these students were confirmed as positive, although critically (as we discuss below) there were a significant number of false positives.
Here is a screenshot of the summary results:
Can we conclude that the true percentage of asymptomatic people with the virus (in the week 1-7 Feb) is 0%. No, because this is only one sample from a large population. If we use all the recent Cambridge data (6 cases from 11,573 people with no symptoms) then we could assume that about 0.052% of people with no symptoms have the virus. However, that data was for different weeks and it is not clear how many of the same students were tested. Fortunately, there is another relevant publicly available dataset for the week of 1-7 Feb that we can use - the data on Premiership football players and staff where we find that only 2 out of 2970 tested positive. Unlike the Cambridge study we cannot be certain that all of the 2970 players and staff tested during the week of 1-7 Feb had no symptoms. Given that footballers are among the few in the population not subject to social distancing it could be argued that (except for people in care homes and hospitals) we ought to see a higher infection rate among them compared to most of the population. If the ONS estimate of 1.25% of the population having the virus during the week of 1-7 Feb were accurate then we might expect to have found 37 cases rather than 2. It is conservative to assume that most of the 2970 did not have symptoms. We do not know if either of the 2 positive cases had symptoms. If they did then (together with the Cambridge study) we could conclude that, of over 7000 people with no symptoms not a single one tested positive. So, let us conservatively assume that the 2 positive cases did not have symptoms. Then, combining the Cambridge and Premier League data we have 2 ‘cases’ from 7,028 people with no symptoms, i.e. 0.0285% of those with no symptoms has the virus.
The two samples are, of course, not representative of the population. However, this sample bias should surely favour the Government claim, because if any group are really likely to have COVID-19 but no symptoms it is surely young and fit people.
What these two samples provide is an estimate of the probability a person has the virus given that they have no symptoms. Using the Government claim of 1.25% probability a person has the virus we can use Bayes Theorem to provide an estimate of the probability a person has no symptoms if they have the virus - which the Government claims is 33% (that's the "1 in 3 claim"). The (Bayesian) 95% confidence interval estimates this probability to be between 1.8% and 7.8% with a mean value of 4.7%. So, instead of 1 in 3 as claimed the figure is between 1 in 56 and 1 in 13, with 'expected value' 1 in 21.
On the other hand if we use the Government "1 in 3" claim, we can also uses Bayes Theorem to estimate the probability
a person has the virus. The
(Bayesian) 95% confidence interval estimates this probability to be
between 0.09% and 0.29% with a mean value of 0.2%, which would suggest the claimed 1.25% infection rate is exaggerated by a factor of over 6.
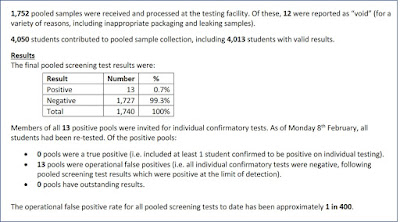
The critical additional information in the Cambridge report is the evidence it provides about false positive tests for people without symptoms as seen in this screenshot:
Critically, the study does pooled testing and then confirmatory testing on each individual case if a pooled test is positive. In the study there were 1752 pooled samples of which 13 were false positives (in the sense that when individual confirmatory testing was done on these, every sample in all 13 pooled samples was negative). So, even in the highly skilled testing environment at Cambridge, the false positive rate (without confirmatory testing) for people without symptoms during the week of 1-7 Feb is 0.7%. This is a much higher rate than the 1 in 400 (0.025%) reported 'to date', but it should be noted that the 1 in 400 rate was also reported for the previous week so it clearly does not take account of the large number of false positives during 1-7 Feb. It is also not clear if the 1 in 400 rate includes confirmatory testing.
The Government 'case' numbers are based on mass PCR testing and there is no evidence that any confirmatory testing has been undertaken as previously reported on this blog. The mass PCR testing will certainly have a higher false positive rate for people with no symptoms than that at Cambridge. This is very important for understanding why the Government 'case' numbers - as well as the "1 in 3" claim are exaggerated. Based on the Cambridge data and some other reasonable assumptions it follows that a high percentage of those without symptoms testing positive are false positives (the report will provide the full Bayesian analysis).
See also:
NFL: All 77 NFL positive covid-19 tests were false positives
Lions' Matthew Stafford glad false-positive led to covid-19 testing change
All COVID-19 articles on this blog



Prof, there is a typo in both the Bayes Theorem calculations; the % sign included in the answer is in error. i.e the answer is correct without the % sign. The text quoting the answer is correct.
ReplyDeleteThanks - you are right. Will fix this and update
DeleteI very much enjoyed your analysis and working through it. Thanks for publishing it. Rgds Andrew
ReplyDeletedata can be made to show whatever you want but basically the goverment has been using scare tactics for so long i dont believe much that comes from official sources , maybe because i am just a sill old 90 year old and heard diferent goverments tell so many lies.I still think the best slogan was COUGHS AND SNEEZES SPREAD DISEASES.
ReplyDeleteNot in a position to confirm or refute the maths, but the Cambridge university study isn't a random sample. It is a sample of a specific subset of the UK population which may well differ significantly from the overall population. The conclusions drawn from 4000+ of the same subset is not the same as the results expected if the same number of people were drawn at random from the UK wide population.
ReplyDeleteYou are right of course. But it can be argued that the bias in the sample should have favoured the Govt claim because if any group are really liekly to have COVID but no symptoms it is surely young people. Same with the footballers in the updated report.
DeleteYes but the Premier League players are in a bubble, following strict protocols to minimise transmission. They are not interacting with the rest of society.
DeleteLike kissing, hugging and spitting throughout the game?
DeleteYes they could catch it during games but as long as they don't go into shops, on public transport etc, covid is unlikely to reach their bubble.
DeleteAlex let me assure you that Professional players DO NOT follow the protocols you speak of,, i know this as a fact because a member of my family and a very good friend are indeed elite footballers, they go to shops, etc
DeleteThis will not be popular with Mr Hancock. Well done.
ReplyDeleteIt has occurred to me that if the Nazis had had the idea of a health pandemic, they could have called the Jews super spreaders, Auschwitz a quarantine camp, and blamed the deaths on the virus.
ReplyDeleteInteresting read. Please note 1 in 400 is 0.25%.
ReplyDeleteOver a year ago, those taken sick on cruise ships, Oceans apart, were the victims of satellite 5G symptoms of blood and respiratory attack. Nothing to do with a virus but treated as such in fear. Michael Gove dismissed 5G and now being rolled out despite having NO Safety certificate. 'The vaccine' is only experimental and only approved under emergency legislation. Beware of the agenda.
ReplyDelete