The impact of misclassifying deaths in evaluating vaccine safety: the same statistical illusion

 In a previous post we showed that if there was a one-week delay in reporting deaths then a vaccine that was a placebo would be seen to have a decreased mortality rate for the vaccinated compared to the unvaccinated. In other words, an illusion of effectiveness is created by the one-week delay in reporting. This is shown in Figure 1 with our hypothetical example comparing the correct figures to the reported figures based on a one-week delay. The example assumes that in this population of 10 million people there is a (constant) weekly mortality rate of 50 deaths per 100,000 people. Each week the population reduces by the number of deaths the previous week. All death numbers (which are simply the relevant population multiplied by 50/100000) are rounded to whole numbers.

Figure 1: Hypothetical example of a placebo vaccine introduced into a population. A) shows correct results; B) shows results reported if there isa one-week delay in reporting deaths

It turns out that, under the same hypothetical assumptions, the same results arise if, instead of a one-week delay in death reporting there is a misclassification of newly vaccinated deaths; specifically, any death of a person occurring in the same week as the person is vaccinated is treated as an unvaccinated, rather than vaccinated, death.

Table 1: Reported deaths and mortality rate if newly vaccinated deaths are reported as unvaccinated

 

A proof of why the results are equivalent (except for week 1) is provided below.

The plot resulting from either reporting error is shown in Figure 2.

Figure 2 Plot of weekly mortality rates under either the delayed death reporting or death misclassification scenarios

It shows the apparently clear life-saving benefit of the ‘vaccine’. 

But there is an obvious indication that these results are not real. If they were, why would the mortality rate in the unvaccinated peak at about the same time as the vaccine programme reaches its peak?

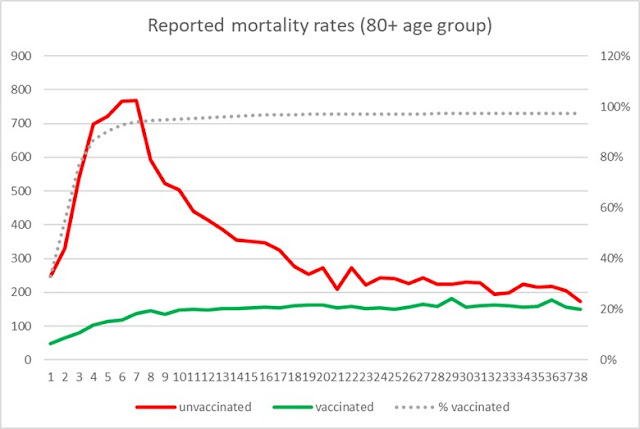
It turns out that the plots for mortality rates from the ONSreport (weeks 1-38) for the Covid-19 vaccination programme in each of the older age categories look remarkably similar to the plot in Figure 2, i.e. with the same peaks in unvaccinated mortality coinciding with when the vaccination programme reached its peak for this age group. For example, Figure 3 shows the 60-69 age group (for which vaccination peak was reached in week 11) and Figure 4 shows the 80+ age groups (for which vaccination peak was reached in week 6).

Figure 3 Plot of weekly mortality rates for Covid19 vaccinated v unvaccinated (this is all-cause mortality but the plots are have hesame shape even if deaths classified as Covid are removed)

 

Figure 4 Plot of weekly mortality rates under either the delayed death reporting or death misclassification

 

Why are the theoretical results important? Because they at least partly explain how the strange observed ONS results could occur even if the mortality rate of the vaccinated was the same (or even higher) than that of the unvaccinated. While it seems that deaths in the ONS report are being reported by date of death (hence are not delayed), newly vaccinated deaths are being classified as unvaccinated. Indeed, it is likely that any death within the first 14 days of vaccination may be classified as unvaccinated.

Moreover, as we will explain in the full analysis that we are currenly preparing, the ONS data provides other clues that suggest different types of errors in reporting. For example, even at the end of the reporting period (when errors such as death misclassification should be minimal and indeed the plots converge) the non-covid mortality rate for the vaccinated is still consistently lower than that of the unvaccinated. This suggests that the proportion of unvaccinated must be systematically underestimated.

 

Proof that, for a population with constant weekly mortality rate, a one-week delay in reporting deaths is equivalent to misclassifying newly vaccinated deaths.

We are assuming that every person who dies in the same week that hey are vaccinated is classified as unvaccinated. Before providing the formal proof, Table 2 provides an informal explanation

Table 2: Informal explanation showing why one week delay in death reporting is equivalent to misclassifying newly vaccinated deaths

week	Total vaccinated (P)	Newly vaccinated (N)	Weekly vaccinated deaths  (A)	Newly vaccinated deaths  (B)	Reported vacc deaths 1-week delay	Reported vacc deaths with misclassification (A-B)
1	10,000	10,000	5	5		0
2	100,000	90,000	50	45	5	5
3	200,000	100,000	100	50	50	50
4	400,000	200,000	200	100	100	100
5	800,000	400,000	400	200	200	200
6	820,000	20,000	410	10	400	400
7	830,000	10,000	415	5	410	410

 

Formal Proof

1.       Let m be weekly mortality rate

2.       Let P_t be total vaccinated at week t

3.       Let N_t be number newly vaccinated in week t. Then N_t=P_t – P_t-1

4.       Let A_t be total number of deaths of vaccinated in week t. So,  A_t=m*P_t

5.       Let B_t the number of deaths of newly vaccinated in week t.  So B_t=m*N_t = m*( P_t – P_t-1) by (3)

6.       The number of reported deaths in week t is A_t – B_t = m*P_t – m*( P_t – P_t-1) = m*P_t-1  by (5) which is the number of actual deaths in week (t-1)